How To Find The Standard Form Of A Parabola

The equation of a parabola can be expressed in either standard or vertex grade as shown in the picture below.

Vertex Class of Equation

The vertex grade of a parabola's equation is mostly expressed every bit: y = a(x-h)²+1000

• (h,k) is the vertex as you tin can encounter in the picture below

  

  

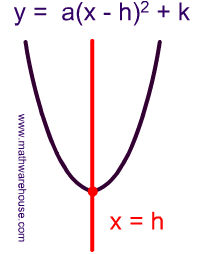
• If a is positive and so the parabola opens upwards like a regular "U".
• If a is negative, then the graph opens downwards like an upside down "U".

• If |a| < ane, the graph of the parabola widens. This merely ways that the "U" shape of parabola stretches out sideways. Explore the mode that 'a' works using our interactive parabola grapher.
• If |a| > 1, the graph of the parabola becomes narrower(The outcome is the contrary of |a| < i).

Practice Bug

Vertex and Direction-Vertex Course Equation

Function I

Problem 1

What is the graph of the following parabola y = (x–1)² + 1?

The parabola'south vertex is the point (1,1).

Problem 2

What is the graph of the following parabola y = –(x–1)² + one?

Problem 3

What is the graph of the following parabola y = (ten+2)² –3?

Identifying the vertex in vertex course

Problem 4.1

What is the vertex of the following parabola: y = (x + iii)² + 4

The vertex is the point (-3,iv)

Trouble 4.2

Find the vertex of the following parabola: y = (x - 3)² + iv

Problem 4.3

What is the vertex of the parabola whose vertex course equation is y = (x - 2)² - 3

Office Two

Trouble 5.one

What is the vertex of a parabola with the following equation:
y = 2(x-3)²+4? Does the parabola open up upwardly or down?

The vertex is (iii,4) and information technology opens upwards since a is positive( information technology is ii), it opens upwards.

Problem v.2

If a parabola'southward equation is y = 3(x+3)² +4, what is its vertex? Which way does it open up?

Vertex = (-iii, four), and it opens upwards since a is positive.

Problem v.3

A parabola has the equation y = -22(x - 9)² + 5. What is its vertex? Which fashion does the parabola open?

Vertex = (ix, 5) and since a is negative (it is -22), information technology opens downwardly.

Source: https://www.mathwarehouse.com/geometry/parabola/standard-and-vertex-form.php

Posted by: torrezandessaint.blogspot.com

Share this post